Shading Analysis
Shading analysis is one of the most essential steps in phase of solar energy system design or analysis. In photovoltaics it is important to analyse shading caused by surrounding objects and/or vegetation. In special cases like analysis or design of BIPV systems, exact analysis of shadow-voltaic systems (overhangs, vertical shading fins, awnings etc.) is also very important. Similar analysis is also part of passive house or solar house design - overhangs must also be planned very carefully in such case. Basic calculations can be done by some simple equations - formulas for some typical simple cases you may find below. Some graphical tools like solar path calculator (pilkington) are also available. For analysis of complex objects several computer tools are available. Some of them offer even 3D simulation. Shading is especially important in photovoltaics. It should be eliminated as much as possible. Even small obstacles like chimneys, telephone poles etc. shouldn't be neglected. To minimise influence of photovoltaic array shading (if shading can not be avoided) different system optimisation techniques can be used.
Shading devices, general
For different simple cases it is in general not difficult to calculate shadows for particular day and time. Below you will find some formulae's end equations which may help you to calculate shadows for most common particular cases in engineering practice.
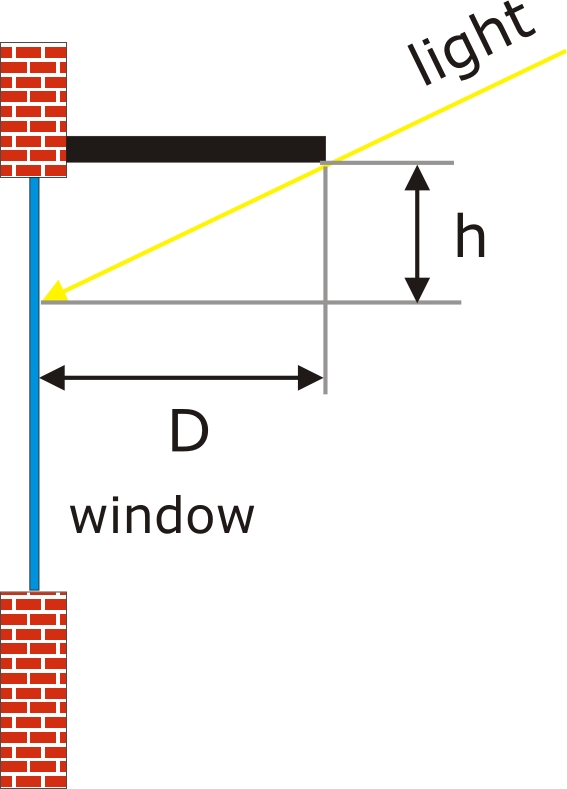
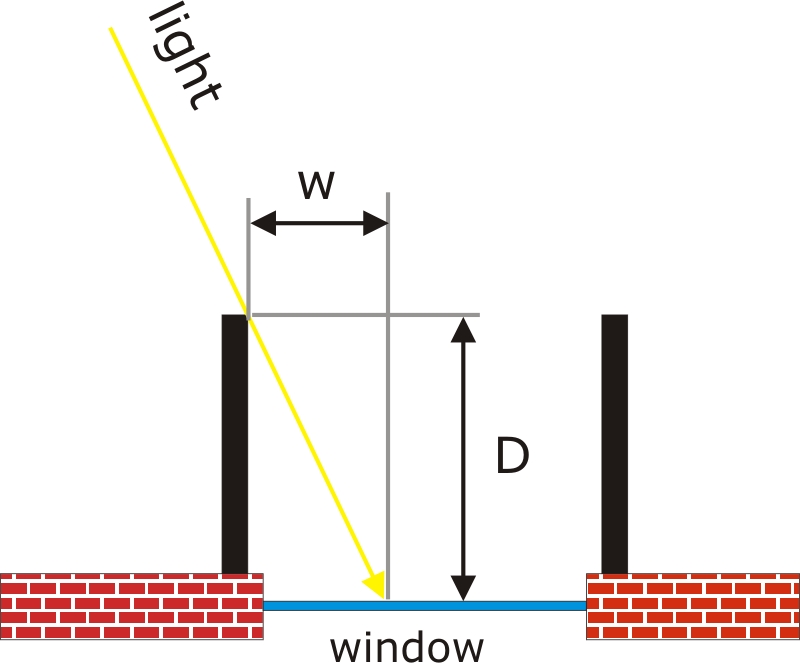
FIGURE 1: Horizontal shading device, overhang, side view (left)
vertical shading device, vertical fin, top view (right)
[Equ 1]
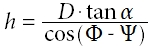
h, D - geometry of horizontal shading device (see Figure 1, left)
α - sun height,
Φ - solar azimuth,
Ψ - plane azimuth
[Equ 2]
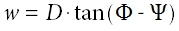
w, D - geometry of vertical shading device (see Figure 1, right)
Φ - solar azimuth, Ψ - plane azimuth
[Equ 3]
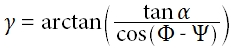
γ = vertical shadow angle (VSA)
w, D - geometry of vertical shading device (see picture above)
Φ - solar azimuth, Ψ - plane azimuth



Solar-Fabrik, solar modules used as shading devices and as part of a facade
image courtesy: Solar-Fabrik AG, Freiburg
Optimization of Strings
Shading losses of photovoltaic systems can not be avoided (if shading occurs), but at least portion of them can be minimised. Right time to consider this issue is the system plannings phase, later it is usually too late. Shading of strings - if crystalline modules are mounted on the roof like on the picture below, they should be always mounted horizontaly (like on the picture) and never vertically. Reason is quite simple: each crystalline module usually includes two bypass diodes which are active if shading occur. When modules are mounted horizontally the module still operates with some amount of power (50 0% or less) if the bottom row is shaded, because only one bypass diod is active. But if modules are mounted vertically and if lower row is shaded partially or completel both bypass diodes are active and amount of output power is close to zero. Strings on the roof, modules oriented horizontaly, souce SSES Preffered orientation of modules in strings on the roof (courtesy SSES). String configuration - modules that are shaded more often than other parts of array should be connected into separate string(s) if possible. This will prevent losses of the whole system because of partial shading of only one part of array.
Inverter configuration
Inverter configuration - some inverter offer several inputs, for each string its own input - in case of shading of one string, other inputs will still operate in MPP.
Amorphous modules
Amorphous modules - in cases where shading can not be avoided use of amorphous modules should be considered. Amorphous modules are far less sensitive on partial shading (in comparison with crystalline modules) so that even in case of partial shading they produce significant amount of power.
Array shape
Array shape - In some cases, like example of the church roof on the picture - you can also prevent shading losse with carefully array design. Array on the picture has shape of trapezoid, because of shading of church's bell tower.



Church's roof covered with photovoltaic roof tiles, optimised array shape
image courtesy: Creaton/Pfleiderer Dachziegel
Tools for Shading Analysis
Solar Pathfinder - The Solar Pathfinder has been the standard in the solar industry for solar site analysis for decades. Its panoramic reflection of the site instantly provides a full year of accurate solar/shade data, making it the instrument of choice.
SunEye™ - The Solmetric SunEye™ (discontinued) is a hand held electronic device that allows users to instantly assess total potential solar energy given the shading of a particular site. Identifying the shading pattern early in the process reduces the expense of system and home design and improves the efficiency of the final system or house.
Steprobotics - accurate solar shade analysis tool. The user attaches a special fish eye lens to the front camera of the phone and converts it into a solmetric sun eye. More information and on-line training.
HORIcatcher - HORIcatcher is an easy and fast tool to take outdoor pictures of the horizon. The pictures can be used to determine the solar energy input, sunshine duration and sun exposure reduced by obstacles like trees, houses or mountains. HORIcatcher is supplied with a digital camera.
Pilkington Sun Angle Calculator - This handy tool provides a relatively simple method of determining solar geometry variables for architectural design, such as designing shading devices or locating the position of the sun relative to a particular latitude and time.
Sonnenbahn Indikator Pro - is a simple tool for site evaluation.
Software
Autodesk ECOTECT Analysis - is an industry leading building analysis program that allows designers to work easily in 3D and apply all the tools neccesary for an energy efficient and sustainable future.
METEONORM - Global Meteorological Database for Solar Energy and Applied Meteorology. METEONORM is a comprehensive climatological database for solar energy applications: a meteorological database containing comprehensive climatological data for solar engineering applications at all points of the globe between the polar circles; a computer program for climatological calculations; a data source for engineering design programs in the passive, active and photovoltaic application of solar energy with comprehensive data interfaces; a standardization tool permitting developers and users of engineering design programs access to a comprehensive, uniform data basis.
Shadow Analyser - Shadow Analyzer is an advanced parametric CAD tool for professionals in the area of Solar Energy Engineering and Architecture.
Shadows - Shadows is a program used to design sundials and astrolabes and it is very useful also in solar energy engineering. Supports plane sundials with polar style of any orientation and reclination, analemmatic sundials, cylindrical and bifilar sundials. Simulates, displays and animates the shadow of the style and offers complete ephemeris of the Sun and draws the Solar Diagram.
pvPlanner - Simulation tool for planning and optimisation of photovoltaic systems using climate and geographic data at high temporal and spatial resolution and new generation high performance algorithms.
Amethyst ShadowFX - Amethyst ShadowFX is a sun and shadow modeling program for architects and town planners. Amethyst ShadowFX enables you to easily generate shadow profiles cast by buildings and other objects for any latitude, longitude and time of year.
Sombrero - A PC-tool to calculate shadows on arbitrarily oriented surfaces. For both, active use of solar energy (domestic hot water, photovoitaics) as well as for passive solar architecture, shading or lighting of planes plays an important role Sombrero provides quantitative results for the shading of collectors or windows by buildings, trees, overhangs or the horizon.
Panorama master - with "Panorama master" you can make exact matched set of photos - base for panorama picture.
Horizon - software simulates sun path diagrams for arbitrary latitude.
GOSOL - Mit dem städtebaulichen Simulationsprogramm GOSOL können städtebauliche Planungen solar+energetisch schnell und zielsicher verglichen, bewertet und optimiert werden.
Additional Information - Books
|
|
Burns, P. J. (1992), Building Solar Gain Modelling; Passive Solar Buildings, Balcomb, J. D., Ed., MIT Press, ISBN 0-262-02341-5. |
|
|
Olgyay, A., Olgyay, V. (1957), Solar Control and Shading Devices, Princeton University Press. |
|
|
Olgyay, V. (1992), Design with climate, Van Nostrand Reinhold, ISBN 0442011105. |
|
|
Mazria, E. (1979), The Passive Solar Energy Book (Expanded Professional Edition), Rodale Press, ISBN 9780878572380. |
|
|
Quaschning, V. (1996), Simulation der Abschattungsverluste bei solarelektrischen Systemen; Verlag Dr. Köster, ISBN: 3-89574-191-4. |
|
|
Szokolay, S. V. (2010), Introduction to Architectural Science, The Basis of Sustainble Design; Architectural Press, ISBN 978-0-7506-8704-1. |
|
|
Tabb, P. (1984), Solar Energy Planning; McGraw-Hill, ISBN 007062688X. |
Additional Information - Papers
|
|
Budin, R., Budin, L. (1982), A Mathematical Model for Shading Calculations; Solar Energy, vol. 29, no. 4, pp 339-349. |
|
|
Dean, E. T. (1979), Graphic methods for determining the solar access design envelope with irregular topography; Proc. 4th National Passive Solar Conference, Kansas City, MO, October 3-5, ASME, p.287. |
|
|
Englund, J. S. (1982), Solar access to residental buildings; Solar Engineering, ASME, p.357. |
|
|
Jones, R. E. (1980), Effects of overhang shading of windows having arbitrary azimuth; Solar Energy, vol. 24, no. 3, pp 305-312. |
|
|
Pongpattana, C., Rakkwamsuk, P. (2006), Efficient algorithm and computing tool for shading calculation, Songklanakarin Journal of Science and Technology, vol.28, no. 2, pp 375-386. |
|
|
Sattler, M. A. et al. (1987), The geometry of the shading of buildings by various tree shapes; Solar Energy vol. 38, no. 3, pp 187-201. |
|
|
Scofield, S. H., Moore, F. (1981), Climatological sundial, Proc. 6th National passive Solar Energy Conference, Portland, OR, September 8-12, ASME, p.382. |
|
|
Sharp, K. (1982), Calculation of monthly average insolation on a shaded surface at any tilt and azimuth; Solar Energy, vol. 28, no. 6, pp 531-538. |
|
|
Sharp, K. (1980), Analytical integration of the insolation on a shaded surface of any tilt and azimuth, Proc. 5th National Passive Solar Energy Conference, Amherst, MA, October 19-26, ASME , p.166. |
|
|
Yanda, R. F., Jones, R. E. (1983), Shading effects of finite width overhang on windows facing toward the equator; Solar Energy, vol. 30, no. 2, pp 171-180. |
|
|
Quaschning, V., Hanitsch, R. (1995), Shade Calculations in Photovoltaic Systems; ISES World Solar Conference - Harare, Zimbabwe. |
|
|
Quaschning, V., Hanitsch, R. (1995), Der Einfluss von Abschatungen auf Photovoltaikanlagen in der Landwirtschaft; 19.Konferenz CIGR Sektion IV, Stuttgart, 25.-28.9. |
|
|
Quaschning, V. (1998), Höhere Flächenausbeute durch Optimierung bei aufgeständerten Modulen; 13. Symposium Photovoltaische Solarenergie · Staffelstein · 11.-13. März. |
Additional Information
|
|
Sustainble by design - Sustainable By Design provides a suite of shareware design tools on sustainable energy topics. |

